运筹学应用场景
指派问题
指派问题(assignment problem)又称分配问题,是一类特殊的 0-1 规划,也是一类特殊的整数规划。有 $n$ 项任务要完成,有 $n$ 项资源(可以理解为人、机器设备等)可以完成任务,并且每项任务交给一个对象完成,每个对象也只能完成一种任务。由于每个对象的特点与能力不同,故其完成各项任务的效率也不同。那么,如何分配资源,才能使完成各项任务的总效率最高(或总消耗最少)? 已知第 $i$ 个人完成第 $j$ 项任务的效率为 $c_{ij}$,$x_{ij}$ 取值 ${0,1}$ 表明是否分配任务,指派问题的一般形式如下:
\[\min z = \sum_{i=1}^n\sum_{j=1}^n c_{ij}x_{ij}\] \[\left\{ \begin{array}{l} \sum_{i=1}^n x_{ij} = 1, \quad j=1,2,\cdots,n \quad \text{第 j 项任务只能由一人完成} \\ \sum_{j=1}^n x_{ij} = 1, \quad i=1,2,\cdots,n \quad \text{第 i 人只能完成一项任务} \\ x_{ij} \in \{0,1\} \end{array} \right.\]其中的矩阵 $\mathbf{C}$ 称为效率矩阵或者系数矩阵。
解法
1955 年,Harold Kuhn 提出了指派问题的解法,他引用了匈牙利数学家 D. Konig 一个关于矩阵中 0 元素的定理,这个解法也就成了匈牙利法。具体可以参考 线性规划及整数线性规划算法
运输问题
运输问题(transportation problem)一般是研究把某种商品从若干个产地运至若干个销地而使总运费最小的一类问题。然而从更广义上讲,运输问题是具有一定模型特征的线性规划问题。它不仅可以用来求解商品的调运问题,还可以解决诸多非商品调运问题。
假定有 $m$ 个产地,$n$ 个销地,令 $a_i$ 为第 $i$ 产地的供应量,$b_j$ 为第 $j$ 销地的需求量,$c_{ij}$ 为从产地 $i$ 到销地 $j$ 的单位运费, 假设 $x_{ij}$ 决策变量为产地 $i$ 到销地 $j$ 的调运数量,如下图所示:
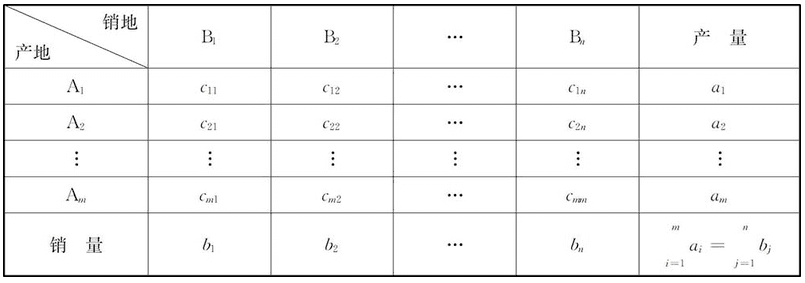
运输问题的数学模型如下:
\[\min z = \sum_{i=1}^m\sum_{j=1}^n c_{ij}x_{ij}\] \[\left\{ \begin{array}{l} \sum_{i=1}^m x_{ij} \ge b_j, \quad j=1,2,\cdots,n \quad \text{输入不能小于销地需求量} \\ \sum_{j=1}^n x_{ij} \le a_i, \quad i=1,2,\cdots,m \quad \text{输出的不能大于产量} \\ x_{ij} \ge 0 \end{array} \right.\]根据总需求量 $\sum_{j=1}^n b_j$ 和总供应量 $\sum_{i=1}^m a_i$ 的关系可以将运输问题划分两类:
- 当 $\sum_{j=1}^n b_j = \sum_{i=1}^m a_i$ 时,为平衡型运输问题;
- 当 $\sum_{j=1}^n b_j \ne \sum_{i=1}^m a_i$ 时,为不平衡型运输问题;
产销平衡运输问题解法
运输问题是一种特殊的线性规划问题,由于其系数矩阵具有特殊的结构,这就有可能找到比一般单纯形法更简便高效的求解方法,即表上作业法,该方法是单纯形法求解运输问题的一种特定形式,其实质是单纯形法
表上作业法计算都可以在产销平衡表中进行,所以该方法叫作表上作业法。 表上作业法是一种迭代算法,其主要步骤是:首先需要确定一个初始调运方案(初始基本可行解),然后检验现行调运方案(现行基本可行解)是否最优,若非最优,则需对现行调运方案(现行基本可行解)进行改进等几个阶段。只是表上作业法对单纯形法做了适当的修改,从而提高了计算的效率。
产销平衡的运输问题一定具有可行解(同时也一定存在最优解),这一点是显然的。确定初始基可行解的方法有很多,一般有最小元素法和伏格尔法(Vogel Method,又称差值法)。
最小元素法即从运价(运距)表中的最小运价(运距)开始,按照“运价(运距)小,先供应”的原则,逐个确定运量。最小元素法的基本思想是就近供应,即从单位运价表中最小的运价开始确定产销关系,依此类推,一直到给出基本方案为止。
最小元素法的缺点:为了节省一处的费用,有时造成在其他多处花几倍的运费。伏格尔法考虑,一产地的产品假如不能按照最小就近供应,就考虑次小供应,这就有一个差额。差额越大,说明不能按照最小运费调运时,运费增加越多,因而对差额最大处,就应当采用最小运费调运。
产销不平衡的运输问题
产大于销的运输问题是在满足需求的前提下,使总运费最小。在实际问题中,产大于销意味着某些产品被积压在仓库中。这样可以把仓库也看成是一个假想的销地,并令其销量刚好等于总产量与总销量的差;那么,产大于销的运输问题就转换成产销平衡的运输问题了。由于假想的销地代表的是仓库,而我们优化的运费是产地与销地间的运输费用,并不包括厂内的运输费用;所以假想列所对应的运价都应取 0。
销大于产的运输问题追求的目标是在最大限度供应的前提下,使总运费最小。同产大于销的问题一样,可以这样设想,假想一个产地,并令其产量刚好等于总销量与总产量的差,由于假想的产地与各销地之间并不存在实际的运输,所以假想的产地行所有的运价都应该是 0,这样就又转换成产销平衡的问题。
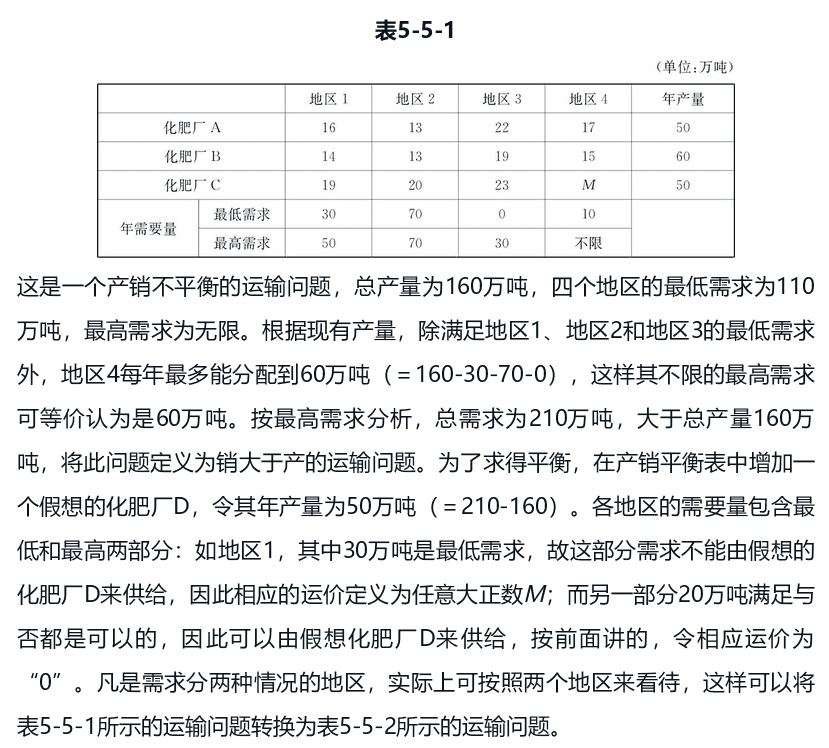
下面是产销不平衡的例子 1:
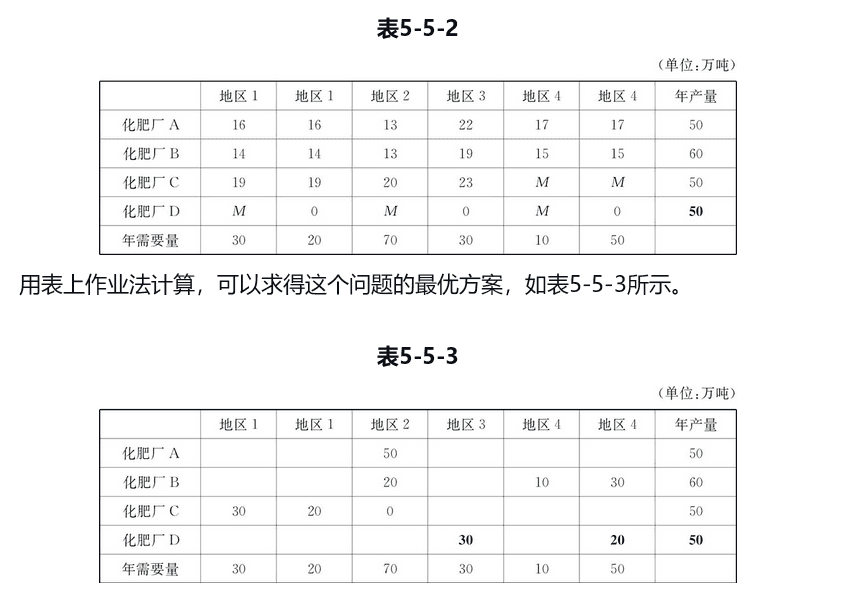
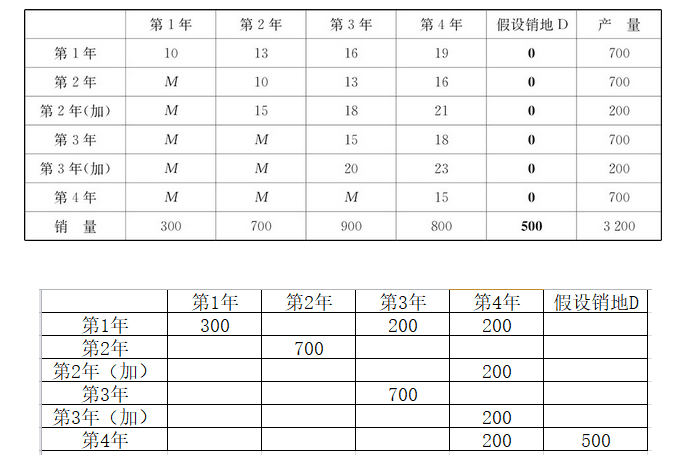
下面是产销不平衡的例子 2:

网络计划技术
网络计划技术起源于美国,是项目计划管理的重要方法。1957 年,美国杜邦化学公司首次采用了一种新的计划管理力法,即关键路线法(critical path method,CPM),1958 年,美国海军武器局特别规划室在研制北极星导弹潜艇时,应用了被称为计划评审技术(program evaluation and review technique,PERT)的计划方法,使北极星导弹潜艇比预定计划提前两年完成。统计资料表明,在不增加人力、物力、财力的既定条件下,采用 PERT 就可以使进度提升 15%-20%,节约成本 10%-15%。
网络计划技术的基本原理是:首先应用网络图来表示工程项目中计划要完成的各项工作,完成各项工作必然存在先后顺序及其相互依赖的逻辑关系,这些关系用节点、箭线来构成网络图。网络图由左向右绘制,表示工作进程,并标注工作名称、代号和工作持续时间等必要信息。通过对网络图进行时间参数的计算,找出计划中的关键工作和关键路线。通过不断改进网络计划,寻求最优方案,以求在计划执行过程中对计划进行有效的控制与监督,保证合理地使用人力、物力和财力,以最小的消耗取得最大的经济效果。
网络计划技术的基本思想就是:通过已知条件绘制出工程项目的网络图,在网络图中找出关键路线和关键工序,利用“向关键路线要时间,向非关键路线要资源”的指导思想,即对各关键工序优先安排资源,挖掘潜力,采取措施,尽量压缩关键工序的时间,从而压缩整个工程项目的完工时间,而对非关键工序,只要在不影响工程完工的前提下,抽出适当的人力、物力等资源,用在关键工序上,以达到缩短工期,合理利用资源的目的。
动态规划问题
动态规划(dynamic programming)是运筹学的一个分支
在工作和生活中,经常会把某些问题的决策过程划分为几个相互联系的阶段,每个阶段都有若干种方案可供选择,而后我们从中选择一个最适合的方案,以获得全过程的最优效益。通常这种问题被称为“多阶段决策问题”,因为各个阶段所采取的决策通常与时间有关,所以也称为动态规划。
1951 年,美国数学家贝尔曼率先提出了动态规划的最优化原理。该原理认为:作为整个过程的最优策略具有这样的性质,即无论过去的状态和决策如何,对前面的决策所形成的状态而言,余下的诸决策必须构成最优策略。这就是说,不管引导到这个现时状态的头一个状态和决策是什么,所有的未来决策应是最优的。通俗来说就是,如果整个策略是最优的,那么其任一子策略也必然是最优的。
目标规划
在一些场景中追求实现一个期望的目标值,比如期望实现利润 100 万元,而不是简单地追求利润最大化,这就需要引入偏差变量
- 负偏差变量 $d^-$:实现值未达到目标期望的偏差值,$d^- \ge 0$;
- 正偏差变量 $d^+$:实现值超过目标期望的偏差值,$d^+ \ge 0$;
这样可以把期望的目标值表达成如下约束条件,我们把它放入约束条件中,称之为目标约束(软约束),模型中原来的约束条件称为系统约束(硬约束),
\[x_1 + x_2 + d^- + d^+ = 1000000\]对于偏差变量 $d^-, d^+$ 至少要有一个为 0,也即 $d^- \dots d^+ = 0$,即只可能出现下面三种情况之一:
- 超额完成利润的目标期望值,$d^+ > 0, \quad d^- = 0$;
- 未能完成利润的目标期望值,$d^- > 0, \quad d^+ = 0$;
- 恰好完成利润的目标期望值,$d^+ = 0, \quad d^- =0 $;
对于目标函数 $f$ 来说,根据决策者的期望可以把 $f$ 写成下面三种形式之一:
- 要求恰好达到目标期望值,$\min f = d^- + d^+$,如果有 $d^- + d^+ = 0$,这就说明恰好实现了目标期望;
- 希望超过目标期望值,即 $\min f = d^-$,这样当 $d^- = 0$ 就是恰好完成了目标;
- 希望不超过目标值,即 $\min f = d^+$,这样当 $d^+ = 0$ 就是恰好完成了目标;
上面介绍的是如何将非求最大最小型的目标转换成软约束和一个目标函数的形式,这是单目标决策优化问题,在现实生活中,优化的目标经常是多元的, 比如既希望完成目标的利润,又希望尽量扩大某种产品的生产,在现实生活也还会看见互相冲突的优化目标,对于这类多目标决策问题, 目标规划的一般处理原则是“系统目标分级、赋权重,决策问题逐级优化求解”,目标分级通过引入“目标优先因子”来实现,赋权重通过引入“相对权重系数”来实现, 这里引入的因子和系数都是需要通过专家评审讨论来提前决定。
比如原有三个目标函数 $\min f_1, f_2, f_3$,其中 $f_1$ 的目标优先级远高于 $f_2, f_3$, 定义两个目标优先因子 $P_1, P_2: P_1 \gg P_2$,这是一个定性的优先关系,表示第一级的目标远比第二级目标重要,它们属于不同层次的目标。 对于 $f_2, f_3$ 属于同级的目标,但是它们之间也是有相对权重,根据评定决定它们对应的相对权重系数为 $w_2, w_3$,汇总在一起得到总体的目标函数如下
\[\min f = P_1 f_1 + P_2 ( w_2 f_2 + w_3 f_3)\]解法
在求解目标规划问题时,按照高优先级的目标优先实现,在其不退化的前提下,再考虑次级目标尽可能实现,这种称为序贯法。
存储论
存储论也称库存论(inventory theory),是研究物资最优存储策略及存储控制的理论。物资的存储是工业生产和经济运转的必然现象。任何工商企业,如果物资存储过多,不但积压流动资金,而且还占用仓储空间,增加保管费用。如果存储的物资是过时的或陈旧的,会给企业带来巨大经济损失;反之,若物资存储过少企业就会失去销售机会而减少利润,或由于缺少原材料而被迫停产,或由于缺货需要临时增加人力和费用。寻求合理的存储量、订货量和订货时间是存储论研究的重要内容。
排队论
排队论(queuing theory),又称随机服务系统理论(random service system theory),是一门研究拥挤现象(排队、等待)的科学。