线性规划及整数线性规划算法

2022-12-04

类别: 自然科学

标签: 算法线性规划单纯形法运筹学

运筹学基础
线性规划
整数线性规划
Python 求解
参考链接

运筹学基础

运筹学中的一套完整的工作流程，可分为如下六个步骤：

问题定义：在实践中遇到的问题，最初可能是模糊的，不精确的，所以第一步就是要把问题明确下来。这一步需要确定研究目标，明确问题边界，列出问题约束和问题要素及其关系；
数据收集：数据收集有可能贯穿研究的全过程，根据研究目标明确需要收集的数据范围，数据既能加深对问题的理解，也是为下一步构建模型提供数据输入；
模型构建：模型是研究对象的抽象，好的模型是保真性、灵活性和成本之间的巧妙平衡，模型需要贴近现实世界的问题，当条件改变时模型也能适应变化，同时模型方便操作和维护；
模型求解：模型求解一般使用计算机软件来完成，需要熟悉成熟模型的算法才好灵活运用；
模型验证：一方面是检查模型是否得到了正确的解，另一方面验证模型的解是否正确反映了问题实际；
结论实施：一般要实施交互式决策服务的工具，同时帮助决策者能够使用和实施，包括提供操作手册和相关培训等，在使用过程中实施全周期管理，当发现原有假设严重偏离时，应重新检验模型并更新工具。

运筹学模型中的三要素：

决策变量（Decision Variables）：待优化的对象；
目标函数（Objective Function）：需要达成的目标的表达式，一般为寻求最大值或最小值，有时候可要求满意、可行、非劣等；
约束条件（Constraints）：表示进行优化时收到的限制，包括资源的限制，时间约束等；

还有模型中的常数项，称为模型的参数（Parameters），参数的取值一般需要收集数据后才能确定。对参数值的不确定性的研究称为灵敏度分析（Sensitivity Analysis）。

线性规划

线性规划用来解决这一类问题：如何使用有限的资源（人力、物力、财力或者时间等）达到一定的目标，很多时候还可能要求以最好的效果来达成目标。

线性指的是模型中所有表达式均为线性等式或不等式，线性规划问题的一般形式如下：

\[\max (\min) z = c_1 x_1\ +\ c_2 x_2\ +\ \cdots \ +\ c_n x_n\] \[\left\{ \begin{array}{lcl} a_{11} x_1\ +\ a_{12} x_2\ +\ \cdots\ +\ a_{1n} x_n &\le (=, \ge)& b_1 \\ a_{21} x_1\ +\ a_{22} x_2\ +\ \cdots\ +\ a_{2n} x_n &\le (=, \ge)& b_2 \\ \qquad \vdots \\ a_{m1} x_1\ +\ a_{m2} x_2\ +\ \cdots +\ \ a_{mn} x_n &\le (=, \ge)& b_m \\ x_1, x_2, \ldots, x_n \le (=, \ge)~0, \text{或无约束} \end{array} \right.\]

标准形式

满足下面 3 个条件的形式为线性规划模型的标准形式，

目标函数最大化；
约束条件等式化；
决策变量非负化；

设线性规划模型中变量数为 $n$ 个，非负约束条件共 $m$ 个，标准形式可写为

\[\max z = c_1 x_1\ +\ c_2 x_2\ +\ \cdots \ +\ c_n x_n\] \[\left\{ \begin{array}{lcl} a_{11} x_1\ +\ a_{12} x_2\ +\ \cdots\ +\ a_{1n} x_n & = & b_1 \\ a_{21} x_1\ +\ a_{22} x_2\ +\ \cdots\ +\ a_{2n} x_n & = & b_2 \\ \qquad \vdots \\ a_{m1} x_1\ +\ a_{m2} x_2\ +\ \cdots +\ \ a_{mn} x_n & = & b_m \\ x_1, x_2, \ldots, x_n \ge 0 \end{array} \right.\]

改写成矩阵形式：

\[\max z = \mathbf{C} \mathbf{X}\] \[\left\{ \begin{array}{l} \mathbf{A} \mathbf{X} = \mathbf{b} \\ \mathbf{X} \ge \mathbf{0} \end{array} \right.\]

其中

\[\mathbf{C} = \left( \begin{matrix} c_1\\ c_2\\ \vdots \\ c_n \end{matrix} \right)^ T,\quad \mathbf{X} = \left( \begin{matrix} x_1\\ x_2\\ \vdots \\ x_n \end{matrix} \right),\quad \mathbf{P_j} = \left( \begin{matrix} a_{1j}\\ a_{2j}\\ \vdots \\ a_{mj} \end{matrix} \right),\quad \mathbf{b} = \left( \begin{matrix} b_1\\ b_2\\ \vdots \\ b_m \end{matrix} \right)\] \[\mathbf{A} = \mathbf{A_{m \times n}} = \left( \begin{matrix} a_{11} & a_{12} & \cdots & a_{1n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{matrix} \right) = (\mathbf{P_1},\mathbf{P_2},\cdots,\mathbf{P_n})\]

其中，$\mathbf{A}$ 称为 $m \times n$ 系数矩阵，一般有 $m < n$，$\mathbf{b}$ 称为资源向量，$\mathbf{C}$ 称为价值向量， $\mathbf{X}$ 称为决策变量向量，$\mathbf{P_j}$ 称为系数列向量。

转换到标准形式的步骤

所有一般形式的线性规划模型都可以转换为标准形式，步骤如下

决策变量非负化：若原变量不是非负化的约束，可以对原变量做加减一个常数值，或者乘以 -1 来转化为非负约束的形式；如果原来是无约束变量如 $x_k$，可以转换成两个带有非负约束的变量 $x_k = x_k’ - x_k’’$，其中 $x_k’, x_k’’ \ge 0$；
约束条件等式化：若约束方程为 $\le$ 可在不等式的左端加入非负松弛变量将不等式转换为等式；若不等式为 $\ge$ 则在左端减去一个非负剩余变量，同样可以转换为等式；
目标函数最大化：若原目标函数是要求最小值，只需要取 $z’ = -z$，就可以转换为求最大值的形式 $\max z’ = (- \mathbf{C}) \mathbf{X}$。

基可行解

区域 $\mathbf{D} = \{ \mathbf{X} \in \mathbf{R}^n\ |\ \mathbf{A} \mathbf{X} = \mathbf{b},\ \mathbf{X} \ge 0 \}$ 称为可行域，若 $\mathbf{X} \in \mathbf{D}$，则称 $\mathbf{X}$ 为可行解（Feasible Solution），若对任意 $\mathbf{X}’ \in \mathbf{D}$，都有 $\mathbf{C} \mathbf{X}’ \le \mathbf{C} \mathbf{X}$，则称 $\mathbf{X}$ 为线性规划问题的最优解。

可以假设系数矩阵 $\mathbf{A}$ 是行满秩（如果不是说明约束条件是线性相关，可以通过变换消去部分约束条件），也即 $\mathbf{A}$ 的秩为 $m$，从而可以从 $\mathbf{A}$ 中找到 $m$ 个线性无关的列向量 $ (\mathbf{P}_{j_1}, \mathbf{P}_{j_2}, \cdots, \mathbf{P}_{j_m}) $，记为 $\mathbf{B}$，称为线性规划问题的一个基（Basis），其中每个向量称为基向量，称对应的决策变量为基变量，其他的变量称为非基变量。

假设 $\mathbf{B}$ 是一个基，可以通过调整变量顺序使得基向量排在前面 $\mathbf{B} = (\mathbf{P}_1, \mathbf{P}_2, \cdots, \mathbf{P}_m)$，设 $\mathbf{N} = (\mathbf{P}_{m+1}, \cdots, \mathbf{P}_n)$，这样导出

\[(\mathbf{B},\ \mathbf{N}) \left( \begin{matrix} \mathbf{X}_{\mathbf{B}} \\ \mathbf{X}_{\mathbf{N}} \end{matrix} \right) = \mathbf{b}\]

因为 $\mathbf{B}$ 是可逆矩阵，可以得出

\[\mathbf{X}_{\mathbf{B}} = \mathbf{B}^{-1} \mathbf{b} - \mathbf{B}^{-1} \mathbf{N} \mathbf{X}_{\mathbf{N}}\]

在上式中令非基变量为 0，这样得到

\[\mathbf{X} = \left( \begin{matrix} \mathbf{X}_{\mathbf{B}} \\ \mathbf{X}_{\mathbf{N}} \end{matrix} \right) = \left( \begin{matrix} \mathbf{B}^{-1} \mathbf{b} \\ \mathbf{0} \end{matrix} \right)\]

满足条件 $\mathbf{A} \mathbf{X} = \mathbf{b}$，称为基解（basic solution），此时如果有 $\mathbf{B}^{-1} \mathbf{b} \ge 0$，则有 $\mathbf{X} \ge 0$ 满足条件，这样的 $\mathbf{X}$ 称为基可行解（Basic feasible solution，BFS），对应的基称为可行基（feasible basis）。他们的关系如下图。

基可行解

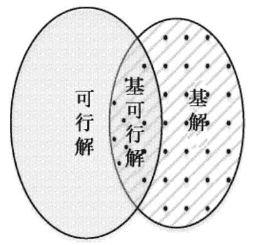
线性规划问题的基最多有 $\binom{n}{m}$ 个（假定任意从 $n$ 个列向量中抽取 $m$ 个都线性无关，则基的数量取到最大值），基解对应于约束条件对应的多面体的交角（corner of the polyhedron），基可行解是位于可行域中的基解。在两个变量的二维平面中，基解就是任意两个约束条件的交点，如下面五个约束条件两两相交对应图中的 $A,B,C,D,E,F,G,H$ 总共 8 个点（有两对直线平行（线性相关）无交点，所以 $\binom{5}{2} - 2 = 8$ ），其中位于可行域中的 $A,B,C,D,E$ 是基可行解，再结合目标函数至少可以找到一个最优解。

\[\left\{ \begin{matrix} x_1&+&2 x_2 &\le& 8 \\ x_1&&&\le& 4 \\ && x_2 &\le& 3 \\ x_1&&&\ge& 0 \\ && x_2 &\ge& 0 \end{matrix} \right.\]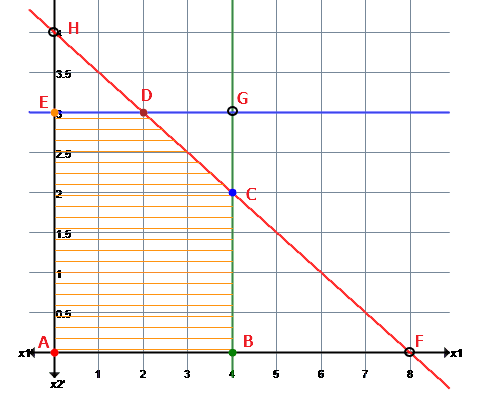

"基解和基可行解"

线性规划的解

关于线性规划问题有下面几个结论：

线性规划问题的可行域如果非空，则一定是凸集；
如果是有界凸集，由于目标函数的连续性，则一定可以在可行域的有界凸集上取得极值，也就是最优解；
在有界可行域的顶点处一定可以找到至少一个最优解；
线性规划问题的基可行解对应于可行域的顶点；（从代数角度定义的“基可行解”和几何角度定义的“顶点”两者本质上是一回事。）

线性规划的解有几种情况：

唯一的最优解；
无穷多最优解；
无界解；
无可行解；

当线性规划问题的可行域非空时，它是有界或无界凸多边形；若线性规划问题存在最优解，它一定在可行域的某个顶点得到；若在两个顶点同时得到最优解，则它们连线上的任意一点都是最优解，即有无穷最优解。

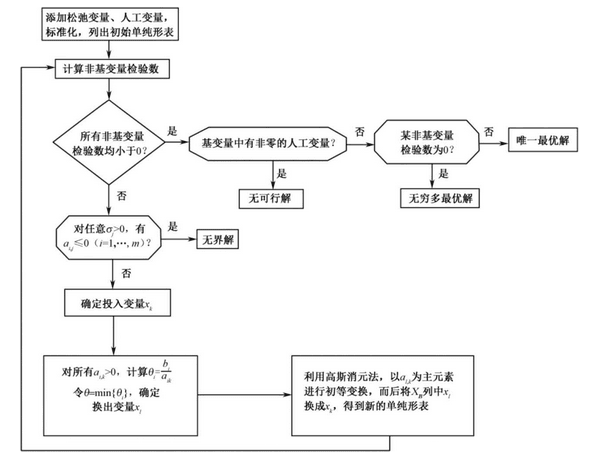
单纯形法

单纯形法（Simplex Method ）是建立在线性规划模型的“标准形式”之上的，总体来说可以分为 5 步：

寻找一个初始解；
构建单纯性表；
判断当前解是否最优；
如果是最优解就结束，不是最优解就换到一个新解上；
在单纯性表中计算相关值，返回第三步重复直到解出最优解或者其他终止条件；

如求解这个例子的单纯行表步骤如下：

\[\max z = 2 x_1 + 3 x_2\] \[\left\{ \begin{matrix} x_1 + 2 x_2 &\le& 8 \\ x_1 &\le& 4 \\ x_2 &\le& 3 \\ x_1,x_2&\ge& 0 \end{matrix} \right.\]

先转换成标准形式如下，以及容易找到一个初始解 $(0,0,8,4,3)^T$

\[\max z = 2 x_1 + 3 x_2\] \[\left\{ \begin{matrix} x_1 + 2 x_2 +x_3 & = & 8 \\ x_1 + x_4 & = & 4 \\ x_2 + x_5 & = & 3 \\ x_1,x_2,x_3,x_4,x_5&\ge& 0 \end{matrix} \right.\]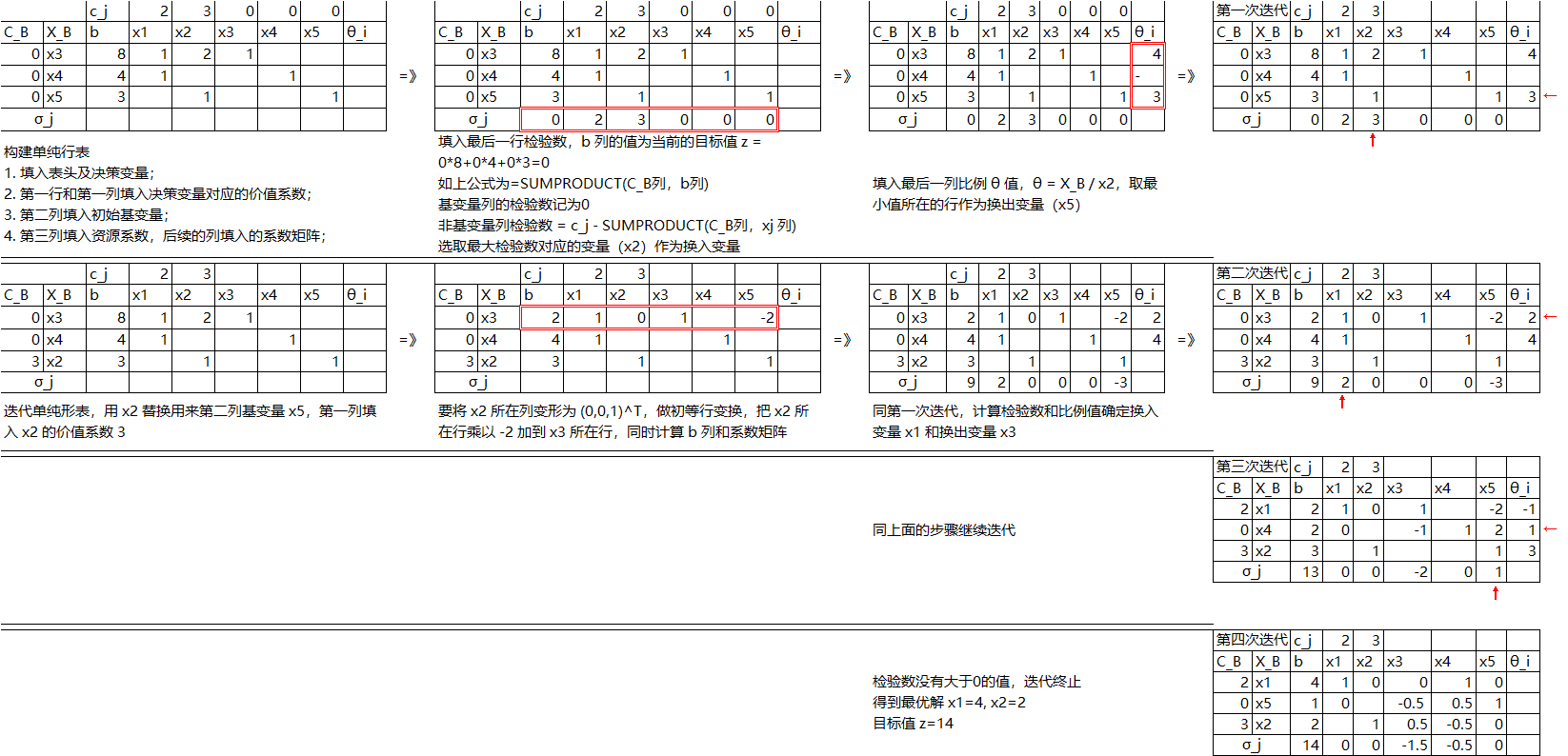

单纯形法

上面步骤中的检验数从下面可以推导出，它代表着目标函数会随着该变量的变化方向，以及变化的快慢，它是资源的影子价格，也被称为边际价格。

\[\begin{array}{rcl} z &=& \mathbf{C} \mathbf{X} \\ &=& \mathbf{C}_{\mathbf{B}} \mathbf{X}_{\mathbf{B}} + \mathbf{C}_{\mathbf{N}} \mathbf{X}_{\mathbf{N}} \\ &=& \mathbf{C}_{\mathbf{B}} (\mathbf{B}^{-1} \mathbf{b} - \mathbf{B}^{-1} \mathbf{N} \mathbf{X}_{\mathbf{N}}) + \mathbf{C}_{\mathbf{N}} \mathbf{X}_{\mathbf{N}} \\ &=& \mathbf{C}_{\mathbf{B}} \mathbf{B}^{-1} \mathbf{b} + ( \mathbf{C}_{\mathbf{N}} - \mathbf{C}_{\mathbf{B}} \mathbf{B}^{-1} \mathbf{N} ) \mathbf{X}_{\mathbf{N}} \end{array}\]

从而对于非基变量 $x_j$ 的检验数为

\[\frac{\partial{z}}{\partial{x_j}} = c_j - \mathbf{C}_{\mathbf{B}} \mathbf{B}^{-1} \mathbf{P}_j = \sigma_j\]

大 M 法

单纯形法开始迭代时需要找到一个初始基可行解，但是上面把线性规划问题转换成标准形式的过程中不能自然得到一个单位矩阵， 大 M 法是在上面转换标准形式的过程中加入人工变量（artificial variables）和惩罚系数如下：

若约束条件为“$\le$”，在不等式左边加入非负松弛变量；
若约束条件为等式，在等式左边加入一个非负人工变量；
若约束条件为“$\ge$”，在不等式左边减去非负剩余变量，再加入一个非负人工变量；
在目标函数中，加入的松弛变量和剩余变量的系数为 0，加入的人工变量系数为 $-M$，是一个任意大的正数，惩罚系数。

如下面的线性规划问题

\[\min z = -3x_1 -2x_2\] \[\left\{ \begin{array} 2x_1 + 4 x_2 - x_3 \le 5 \\ -x_1 + x_2 - x_3 \ge -1 \\ -x_2+x_3 = 1 \\ x_1,x_2,x_3 \ge 0 \end{array} \right.\]

用大 M 法转成标准形式：

\[\max z = 3x_1 + 2x_2 - M x_6\] \[\left\{ \begin{array}{rcccl} 2x_1 + 4 x_2 - x_3 &+ x_4 &&&= 5 \\ x_1 - x_2 + x_3 &&+ x_5 & &= 1 \\ -x_2+x_3 &&&+ x_6 &= 1 \\ x_1,x_2,x_3,x_4,x_5,x_6 &&&&\ge 0 \end{array} \right.\]

其中 $x_6$ 是人工变量，这样可以得到 $x_4,x_5,x_6$ 的系数列向量构成单位矩阵 $\mathbf{B}$，初始基解 $\mathbf{X} = (0,0,0,5,1,1)^T$ 为基可行解，从而开始单纯形法计算。

这里可以得到线性规划问题四种解的判别准则：

唯一的最优解：对于所有非基变量，检验数都有 $\sigma_j < 0$；
无穷多最优解：对于所有非基变量，检验数都有 $\sigma_j \le 0$，且存在某个非基变量的检验数等于 0；
无界解：存在一个非基变量的检验数 $\sigma_{m+k} > 0$，且该变量在系数矩阵中对应的列 $\mathbf{P}_{m+k} \le 0$；
无可行解：满足上面的迭代终止条件，但是存在取非零值的人工变量，则此线性规划问题无可行解；

单纯形法的计算流程

两阶段法

大 M 法在用计算机求解的过程中 M 值一般用很大的数来近似替代，这会造成计算上的累计误差，两阶段法就是用拆分成两个阶段的办法来解决这个问题，使得计算过程中不出现大 M。

第一阶段用来寻找一个不包含人工变量的初始基可行解。步骤是在原问题引入松弛变量和人工变量进行标准化，构造仅含人工变量的目标函数，将其价值系数设置为 -1，使用单纯形法求解，若得到了目标函数为 0，也即是得到了不包含人工变量的一个基可行解，从而转入第二阶段，否则原问题无可行解。

第二阶段，使用第一阶段得到的最终单纯形表，去掉其中的人工变量，并将目标函数还原成原问题的目标函数，继续使用单纯形法求解即可。

例子，线性规划问题如下

\[\max z = -4 x_1 - x_2 +2x_3\] \[\left\{ \begin{array}{c} x_1 -2x_2+x_3 \le 11 \\ -4x_1+x_2 + 2x_3 \ge 3 \\ -2x_1 + x_3 = 1 \\ x_1,x_2,x_3 \ge 0 \end{array} \right.\]

第一阶段，转换成带人工变量的标准形式，用单纯形法第一次迭代 $x_3$ 替换掉 $x_7$，第二次 $x_2$ 替换掉 $x_6$，这样第一阶段就结束了。

\[\max w = -x_6 - x_7\] \[\left\{ \begin{array}{c} x_1 - 2x_2+x_3+x_4 = 11 \\ -4 x_1 + x_2 +2x_3 - x_5 + x_6 = 3 \\ -2x_1 + x_3 + x_7 = 1 \\ x_1,x_2,x_3,x_4,x_5,x_6,x_7 \ge 0 \end{array} \right.\]

退化情形与勃兰特准则

在单纯形法的求解中可能出现 $\theta$ 为 0 的情形，即该行的资源系数为 0，称这种情况是退化的。出现退化的情形是因为约束条件中存在线性相关的条件。

出现退化的情况可能导致迭代出现局部循环，而最优解不在其中。解决的办法就是使用勃兰特准则（Bland’s rule）：

换入变量不用检验数最大的那个，而是用大于 0 的检验数中下标最小的决策变量；
换出变量还是使用 $\theta$ 最小的那个，如果有出现两个以上的相同最小值，使用下标最小的决策变量作为换出变量。

内点法

1984 年 AT&T Bell 实验室一位年轻的数学家 Narendra Karmarkar 发明了求解线性规划的问题的新算法，它在解特大型线性规划问题方面有巨大的潜力。 Karmakar 算法也是一种迭代算法，它从得出一个可行的实验解开始，在每次迭代中，它在可行域内从当前实验解开始移动到另一个更好的实验解，然后继续这个过程直到实验解（基本上）达到最优解为止。对单纯形法所有的移动都是在可行域的边界上进行的，而 Karmarkar 算法实验解是内点（interior point），所以也被称为内点法（interior-point algorithm）。

因为内点法获得专利的早期版本被称为障碍点算法，故内点法也被称为障碍算法（barrier algorithm），“障碍”一词是因为从搜索的角度看所找的实验解都是内点，每一个约束边界都被作为障碍对待。

内点法比单纯形法复杂，它的每一次迭代都需要大量的迭代去寻找下一个实验解，因此内点法每次迭代的时间是单纯形法的好几倍。对于非常小的问题，内点法需要的迭代次数和单纯形法差不多，这样对于小规模问题内点法速度上不如单纯形法。但是对于大规模的问题，比如 10000 个约束条件的问题可能只需要 100 次以下迭代，相反单纯形法可能需要 20000 次迭代，这样考虑上内点法每次迭代上多消耗的时间，总体时间内点法还可能更短一些。内点法和单纯形法也可以结合使用。

整数线性规划

在上述的线性规划问题的基础上，如果要求某些决策变量或者全部决策变量要求为整数，则称这样的问题为整数规划问题（Integer Programming，IP），除了整数约束条件外其他的部分称为相应的松弛问题（Slack Problem）。如果所有决策变量要求为整数称为纯整数规划（Pure Integer Programming）或全整数规划（All Integer Programming）。如果只是部分决策变量要求为整数，则称为混合整数规划（Mixed Integer Programming，MIP）。整数规划中如果所有决策变量要求取值只能是 0 或者 1，称为 0-1 型整数规划问题。有一类特殊的 0-1 整数规划问题称为指派问题（assignment problem），有 n 项任务要完成，有 n 项资源（可以理解为人、机器设备等）可以完成任务，并且每项任务交给一个对象完成，每个对象也只能完成一种任务。由于每个对象的特点与能力不同，故其完成各项任务的效率也不同。那么，如何分配资源，才能使完成各项任务的总效率最高（或总消耗最少）？指派问题的一般形式如下：

\[\min z = \sum_{i=1}^n\sum_{j=1}^n c_{ij}x_{ij}\] \[\left\{ \begin{array}{l} \sum_{i=1}^n x_{ij} = 1, \quad j=1,2,\cdots,n \quad \text{第 j 项任务只能由一人完成} \\ \sum_{j=1}^n x_{ij} = 1, \quad i=1,2,\cdots,n \quad \text{第 i 人只能完成一项任务} \\ x_{ij} \in \{0,1\} \end{array} \right.\]

其中的矩阵 $\mathbf{C}$ 称为效率矩阵或者系数矩阵。

下面是整数线性规划问题的几个主要求解算法：

分枝定界法：可求纯或混合整数线性规划。
割平面法：可求纯或混合整数线性规划。
隐枚举法：用于求解 0-1 整数规划。
匈牙利法：解决指派问题（0-1 规划特殊情形）。
蒙特卡罗法：求解各种类型规划。

分枝定界法

分枝定界法（Branch and Bound, B&B）在 20 世纪 60 年代初由 A.H.Land 和 A.G.Doig 两位学者提出，用于解纯整数或混合整数规划问题。

它的基本思路是考虑到整数规划可行解中任何相邻整数之间的区域均不含整数解，这样就可以将松弛问题的可行域分为多个分枝，同时将求解整数规划问题转化为求解多个线性规划的问题。

假设整数线性规划问题 A，去掉其中的整数约束得到的松弛问题 B，分枝定界法的基本步骤如下：

解出问题 B，可能出现下面解的情况
1. B 无可行解，则 A 无可行解，停止计算；
2. B 有最优解，并符合 A 的整数约束条件，则此最优解就是 A 的最优解，停止计算；
3. B 有最优解，但不符合 A 的整数约束条件，记此最优解的目标函数值为 $\overline{z}$；
分枝：选出 B 最优解中任一不符合整数约束的变量 $x_j$，其值为 $b_j$，构造两个约束条件 $x_j \le [b_j]$ 和 $x_j \ge [b_j] + 1$ 添加到 B 中，形成两个分枝问题 B1 和 B2；
定界：求解 B1 和 B2 问题，从最优目标函数值最大者作为新的上界 $\overline{z}$，从已符合整数约束的分枝中找出目标函数最大者作为新的下界 $\underline{z}$；
剪枝：各分枝的最优目标如果小于 $\underline{z}$，则剪掉这个分枝，若大于 $\underline{z}$ 且不符合整数条件则重复第二步继续分枝；

问题 1	问题 2	说明
无可行解	无可行解	整数规划无可行解
无可行解	整数解	此整数解即最优解
无可行解	非整数最优解	对问题 2 继续分枝
整数解	整数解	目标值最大的为最优
整数解，目标值优于问题 2	非整数最优解	问题 1 整数解即为最优解
整数解，目标值不如问题 2	非整数最优解	问题 1 停止分枝，它的目标值作为下界，对问题 2 继续分枝

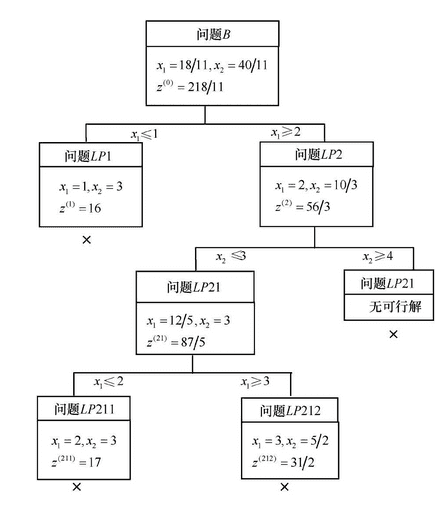
如用分枝定界法求解下面例子

\[\max z = x_1 + 5 x_2\] \[\left\{ \begin{array}{c} x_1 - x_2 \ge -2 \\ 5x_1+6x_2 \le 30 \\ x_1 \le 4 \\ x_1,x_2 \ge 0 \text{且全为整数} \end{array} \right.\]

第一步求解松弛问题，得到最优解： $x_1=\frac{18}{11},\quad x_2=\frac{40}{11},\quad z=\frac{218}{11}$

显然有 $x_1=0, x_2=0$ 是满足规划问题的一个整数解，这样得到一个上界和下届，$0 \le z \le \frac{218}{11}$。

对 $x_1 = \frac{18}{11}$ 进行分枝，构造两个约束条件 $x_1 \le 1$ 和 $x_1 \ge 2$，得到两个问题 LP1 和 LP2，求解得到两个最优解：

\[x_1 = 1, x_2 = 3, z = 16 \quad \text{对应问题 LP1}\] \[x_1 = 2, x_2 = \frac{10}{3}, z = \frac{56}{3} \quad \text{对应问题 LP2}\]

分枝 LP1 停止分枝，得到新的下界 16，分枝 LP2 给出新的上界 56/3，选择 $x_2$ 对 LP2 继续分枝，如下：

"分枝定界法"

割平面法

割平面法是 1958 年 R.E.Gomory 提出的，也称为 Gomory 割平面法，它的基本思想是不考虑整数要求，先求解松弛问题的解，如果没有得到满足整数要求的解，那么逐次增加一个新约束（即割平面），割掉原可行域的一部分（只含非整数解），使得切割后最终得到这样的可行域（不一定一次性得到），它的一个有整数坐标的顶点恰好是问题的最优解。切割方程由松散问题的最终单纯形表中含非整数解基变量的等式约束演变而来。

割平面法是在松弛问题的可行域的边缘不断地添加割平面切掉不含整数解的部分，从而不断逼近整数解，而分枝定界则是直接将可行域从整数处切成两个分枝部分再分别求解。

隐枚举法

隐枚举法（implict enumeration）：只检查变量取值组合的一部分，就能求得问题的最优解的方法。

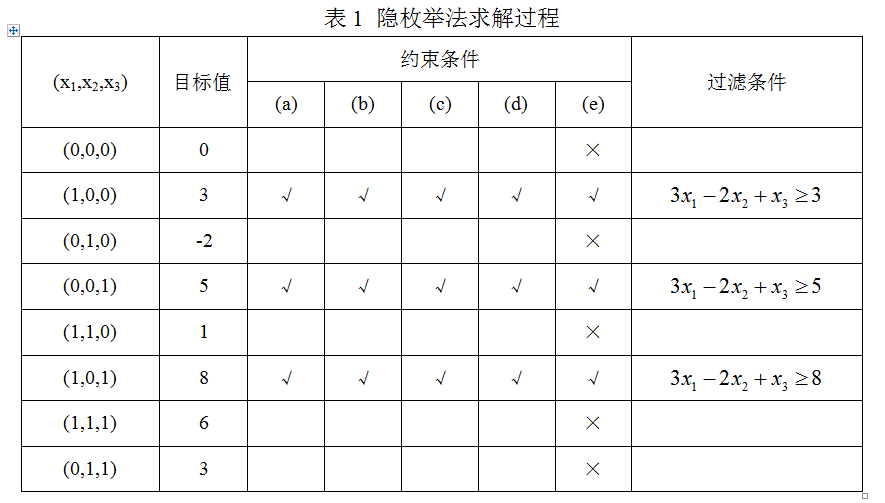
例子如求解如下问题

\[\max z = 3x_1 -2x_2+5x_3\] \[\left\{ \begin{array}{l} x_1+2x_2-x_3 \le 2 \\ x_1+4x_2+x_3 \le 4 \\ x_1+x_2 \le 3 \\ 4x_1+x_3 \le 6 \\ x_1,x_2,x_3 \in \{0,1\} \end{array} \right.\]

先试探得到 $(1,0,0)$ 是一个可行解，计算出目标函数值 $z=3$，结合目标函数可以增加约束条件 $3x_1 -2x_2+5x_3 \ge 3$，这个条件称为过滤条件（filtering constraint），这样，原问题的线性约束条件就变成 5 个。用穷举法，3 个变量共有 8 个解。对每个解，依次代入 5 个约束条件左侧，先判断是否满足过滤条件，如果不满足就可以直接跳过，满足后再检查后面约束条件，如果都满足且得到了更好的目标值则更新过滤条件的值，这样继续如下表所示：

"隐枚举法"

匈牙利法

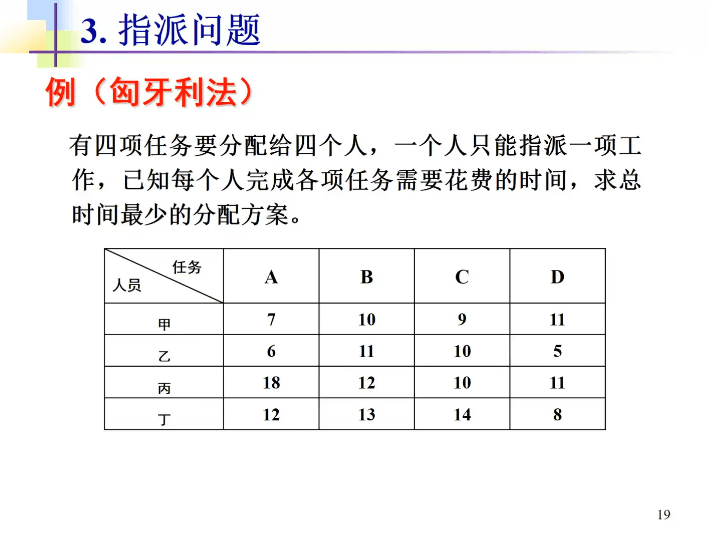
匈牙利法是基于指派问题的标准型，标准型需要满足下面 3 个条件：

目标函数求最小 min；
效率矩阵为 n 阶方阵；
效率矩阵所有元素 $c_{ij} \ge 0$，且为常数；

"匈牙利法"

"匈牙利法例子"

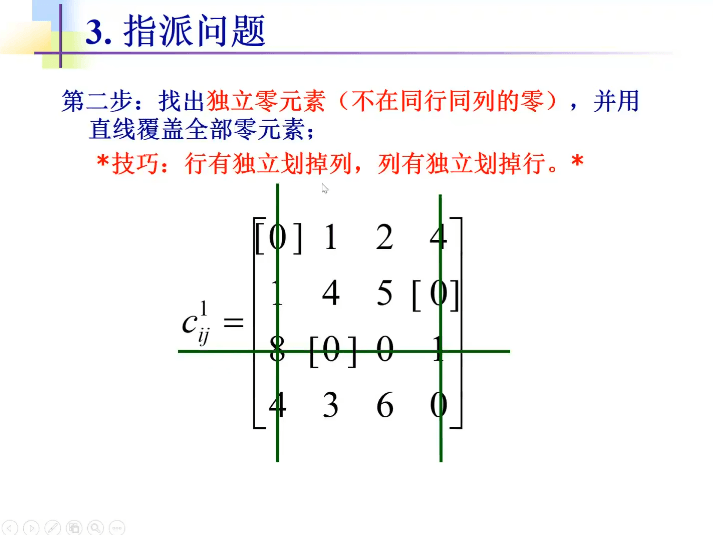
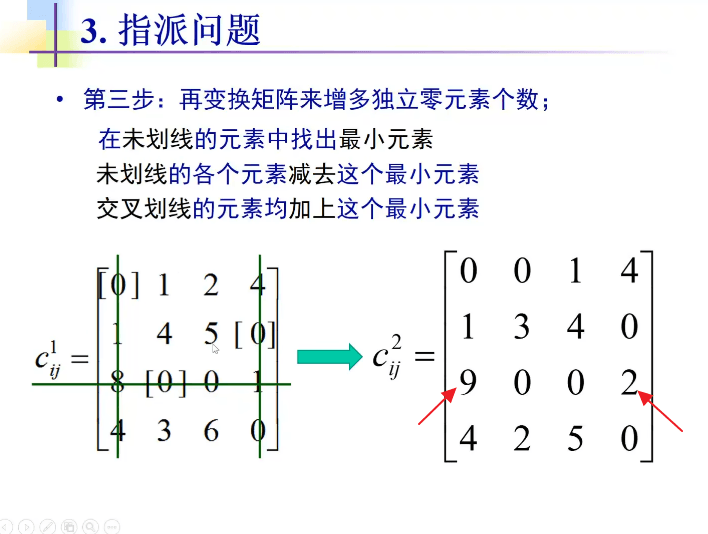
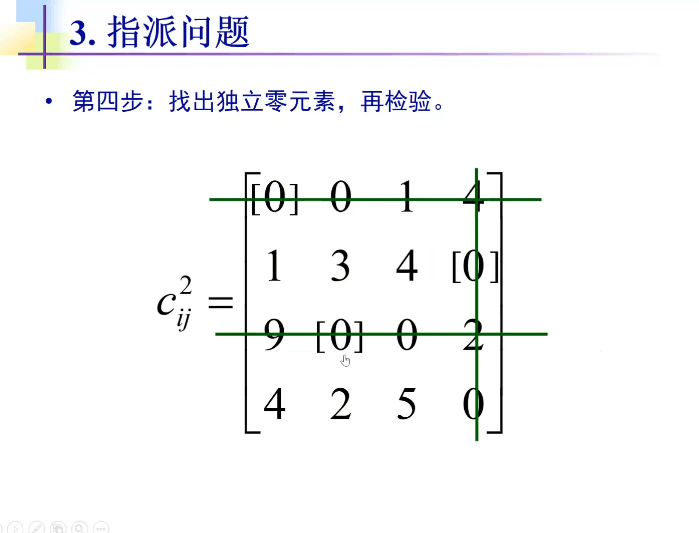
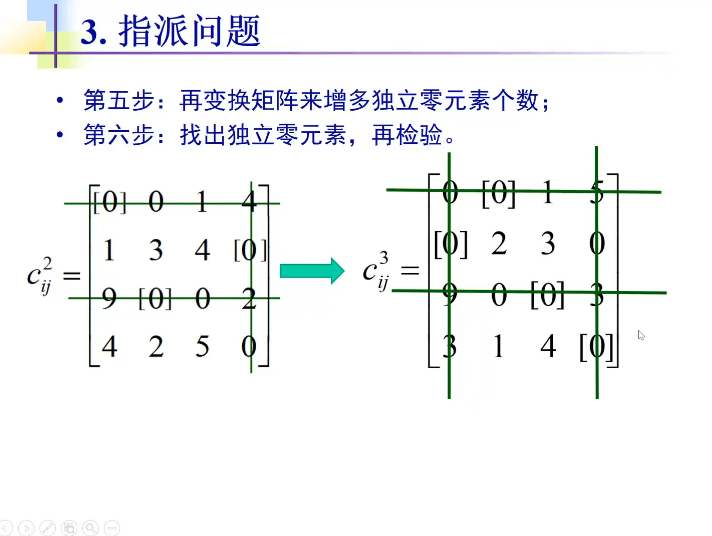
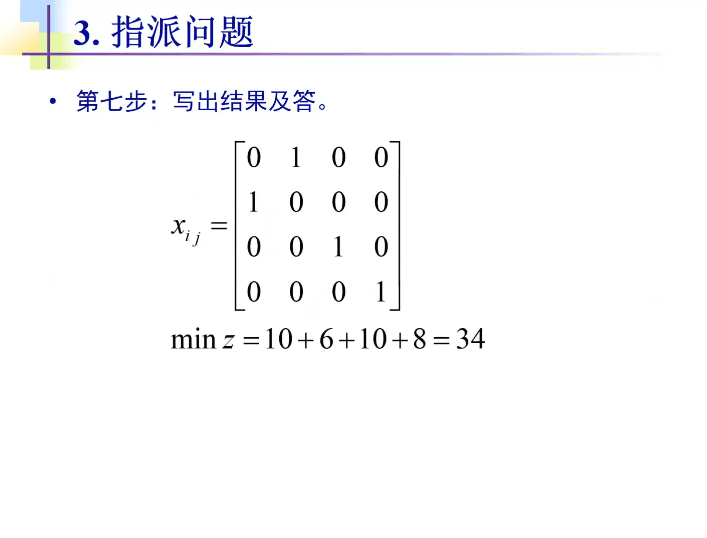
对于非标准形的指派问题，可以转换成标准形式： "匈牙利法例子"

蒙特卡洛法

蒙特卡罗法就是选择部分穷举法，随机取样来得到在有限取样下的一个最优解。

Python 求解

线性规划问题的求解主要依赖下面两个包：

SciPy：Python 的一个通用科学计算包；
PuLP：提供 Python 的定义线性规划问题的 API 接口，并调用外部的求解器求解；

线性规划问题求解

用 SciPy 来求解上面的线性规划问题：

import scipy
scipy.__version__
# '1.9.1'

import numpy as np
from scipy import optimize

# 定义参数，因为是算法是求最小值，需要把价值系数乘以 -1
c= np.array([-2, -3])
A_ub=np.array([[1,2],[1,0],[0,1]])
b_ub=np.array([8,4,3])
x0_bound=(0,None)
x1_bound=(0,None)

# 用单纯型法求解，得到最优解 [4,2] 和最优目标值 14
res = optimize.linprog(c, A_ub=A_ub, b_ub=b_ub,bounds=[x0_bound, x1_bound], method='simplex')
print(res)
#      con: array([], dtype=float64)
#      fun: -14.0
#  message: 'Optimization terminated successfully.'
#      nit: 3
#    slack: array([0., 0., 1.])
#   status: 0
#  success: True
#        x: array([4., 2.])


# 使用默认的 HiGHS 算法求解
optimize.linprog(c, A_ub=A_ub, b_ub=b_ub,bounds=[x0_bound, x1_bound])
#            con: array([], dtype=float64)
#  crossover_nit: 0
#          eqlin:  marginals: array([], dtype=float64)
#   residual: array([], dtype=float64)
#            fun: -14.0
#        ineqlin:  marginals: array([-1.5, -0.5, -0. ])
#   residual: array([0., 0., 1.])
#          lower:  marginals: array([0., 0.])
#   residual: array([4., 2.])
#        message: 'Optimization terminated successfully. (HiGHS Status 7: Optimal)'
#            nit: 1
#          slack: array([0., 0., 1.])
#         status: 0
#        success: True
#          upper:  marginals: array([0., 0.])
#   residual: array([inf, inf])
#              x: array([4., 2.])

现在 SciPy 的线性规划问题默认使用 HiGHS 求解，HIGHS 是用 C++ 写的一个求解软件，提供 C, C#, FORTRAN, Julia and Python 的接口。

HiGHS - high performance software for linear optimization

Open source serial and parallel solvers for large-scale sparse linear programming (LP), mixed-integer programming (MIP), and quadratic programming (QP) models

HiGHS 的 GitHub 地址，Wiki 地址，论文地址。它主要是两个并行对偶单纯形求解器（PAMI 和 SIP）的设计和实现。

整数线性规划问题求解

用 SciPy 来求解上面的整数线性规划问题，加上 integrality 参数即可， 0 表示连续变量，无整型约束，1 表示整数约束，其他参考文档。

import numpy as np
from scipy import optimize

# 定义参数，因为是算法是求最小值，需要把价值系数乘以 -1
ip_c= np.array([-1, -5])
ip_A_ub=np.array([[-1,1],[5,6],[1,0]])
ip_b_ub=np.array([2,30,4])
ip_x0_bound=(0,None)
ip_x1_bound=(0,None)
ip_integrality=np.array([1,1])

# 加上整数约束求解，得到最优解 [2,3] 和最优目标值 17
optimize.linprog(ip_c, A_ub=ip_A_ub, b_ub=ip_b_ub,bounds=[ip_x0_bound, ip_x1_bound], integrality=ip_integrality)
#            con: array([], dtype=float64)
#  crossover_nit: -1
#          eqlin:  marginals: array([], dtype=float64)
#   residual: array([], dtype=float64)
#            fun: -17.0
#        ineqlin:  marginals: array([0., 0., 0.])
#   residual: array([1., 2., 2.])
#          lower:  marginals: array([0., 0.])
#   residual: array([2., 3.])
#        message: 'Optimization terminated successfully. (HiGHS Status 7: Optimal)'
#            nit: -1
#          slack: array([1., 2., 2.])
#         status: 0
#        success: True
#          upper:  marginals: array([0., 0.])
#   residual: array([inf, inf])
#              x: array([2., 3.])

0-1 规划问题求解

用 SciPy 来求解上面的 0-1 规划问题。

import numpy as np
from scipy import optimize

# 定义参数，因为是算法是求最小值，需要把价值系数乘以 -1
zo_c= np.array([-3, 2,-5])
zo_A_ub=np.array([[1,2,-1],[1,4,1],[1,1,0],[4,0,1]])
zo_b_ub=np.array([2,4,3,6])
zo_x0_bound=(0,1)
zo_x1_bound=(0,1)
zo_x2_bound=(0,1)
zo_integrality=np.array([1,1])

# 加上整数约束求解，得到最优解 [1,0,1] 和最优目标值 8
optimize.linprog(zo_c, A_ub=zo_A_ub, b_ub=zo_b_ub,bounds=[zo_x0_bound, zo_x1_bound,zo_x2_bound], integrality=zo_integrality)
#            con: array([], dtype=float64)
#  crossover_nit: -1
#          eqlin:  marginals: array([], dtype=float64)
#   residual: array([], dtype=float64)
#            fun: -8.0
#        ineqlin:  marginals: array([0., 0., 0., 0.])
#   residual: array([2., 2., 2., 1.])
#          lower:  marginals: array([0., 0., 0.])
#   residual: array([1., 0., 1.])
#        message: 'Optimization terminated successfully. (HiGHS Status 7: Optimal)'
#            nit: -1
#          slack: array([2., 2., 2., 1.])
#         status: 0
#        success: True
#          upper:  marginals: array([0., 0., 0.])
#   residual: array([0., 1., 0.])
#              x: array([1., 0., 1.])

指派问题求解

用 SciPy 来求解上面的指派问题：

from scipy.optimize import linear_sum_assignment

# 定义效率矩阵
cost = np.array([[7,10,9,11], [6,11,10,5], [18,12,10,11],[12,13,14,8]])

# 指派问题求解
row_ind, col_ind = linear_sum_assignment(cost, maximize=False)

col_ind
# array([1, 0, 2, 3], dtype=int64)

cost[row_ind, col_ind].sum()
# 34